iron in condiments

2. Spectrometric determination of iron
in dry condiment samples

OBJECTIVE

To prepare a calibration curve and determine the content of iron in condiment samples.

THEORETICAL BACKGROUND

Iron is part of hemoglobin, the oxygen-carrying complex protein of the blood, and myoglobin, which helps muscle cells store oxygen. Iron-deficient people tire easily because their bodies are starved for oxygen.

The most absorbable form of iron, called “heme” iron, is found in oysters, meat, poultry, and fish. Non-heme iron is also found in these foods, as well as in dried fruit, molasses, leafy green vegetables, wine, and condiments.

A method for the determination of iron in condiments consists of dry ashing of a sample in a crucible, dissolving the residue in dilute hydrochloric acid, forming the complexes of iron(III) ions with thiocyanate ions and measuring the transmittance of coloured complexes. Iron(III) forms with thiocynate a series of orange-red complexes which are not very stable. The first step of the reaction is presented below. Complexes with up to six thiocyanate ligands can be formed.

Fe³⁺(aq) + SCN^-(aq) D	Fe(SCN)²⁺(aq)
	orange-red thiocyanate complex

Thiocyanate is one of the oldest reagents for determination of iron (III) ions in different samples. It is neither very sensitive nor very selective. We selected this reagent, since it is readily available.

EQUIPMENT AND REAGENTS

A Spektra^TM spectrometer,
dry condiment samples: e.g. basil, thyme, marjoram,
0.05 M solution of iron(III) chloride (0.6705 g of FeCl₃ . 6 H₂O per 50 mL of solution),
0.1 M solution of KSCN,
2 M solution of HCl,
crucible, micropipette, burner and ring stand, water bath, filter paper with fine porosity, glass funnel, funnel rack, laboratory stand, glass rod, glass vials with caps.

HAZARDS

	Hydrochloric acid is corrosive and toxic: it causes severe irritation of the upper respiratory tract and is harmful if absorbed through the skin. Avoid inhalation and skin contact. R: 24/25-34, S: 28.2-45

	Potassium thiocyanate Ingestion and inhalation may cause irritation of the digestive and respiratory tracts. May be harmful if swallowed. It can also cause skin irritation and may be absorbed through the skin in harmful amounts. R: 20/21/22-32, S 13
	Iron(III) chloride hexahydrate causes chemical burns to the respiratory tract. It can also cause skin burns, and when in contact with acids it liberates toxic gases. R: 31-34, S: 28-45-50.1

PROCEDURE

Preparation of a condiment sample:

Weigh a clean and dry crucible.
Grind and homogenize condiment samples.
Weigh 1 g of a condiment sample in a crucible.
With the burner start slowly heating the crucible with the sample. After reduction of the volume, ignite the sample until a white or grey ash with no black particles is obtained (for basil one and a half hour will do, other samples will need more time).
After completion of the ignition, let the crucible cool down to room temperature.
Weigh the crucible with the ash sample.
Add 5 mL of 2 M HCl into the crucible.
Dry the content of the crucible on a water bath.
Cool down and add 3 mL of deionised water, 5 mL of 2 M HCl and 5 mL of 0.1 M KSCN.
Filter the sample solution through a filter paper with fine porosity. Discard the first third of the filtrate and collect the other part in a clean and dry glass vial with a cap.

Preparation of a diluent solution and a stock solution of iron(III) thiocianate complex:

Prepare a diluent solution by mixing in a dry and clean vial 3 mL of deionising water, 5 mL of 0.1 M KSCN, and 5 mL of 2 M HCl.
Prepare a stock solution of an iron (III) thiocyanate complex in a dry and clean vial by mixing 0.5 mL of 0.05 M FeCl₃ solution with 2.5 mL of deionised water and 5 mL of 0.1 M KSCN solution, and 5 mL of 2 M HCl.

Spectrometric measurement

Prepare a blank, sample(-s) and a series of calibration solutions on a blister as follows:

	g(Fe³⁺) [mg/L]	Stock solution of the complex V [mL ]	Diluent solution V [mL ]	Sample solution V [mL ]
Blank	-	0	450	-
Sample	-	-	-	450
Calibration solution 1	12.1	50	400	-
Calibration solution 2	24.3	100	350	-
Calibration solution 3	36.4	150	300	-
Calibration solution 4	48.6	200	250	-
Calibration solution 5	60.7	250	200	-
Calibration solution 6	72.9	300	150	-
Calibration solution 7	85.0	350	100	-
Calibration solution 8	97.2	400	50	-
Calibration solution 9	109.3	450	0	-

Insert a blister into the measuring chamber of a Spektra^TM spectrometer so that a blank solution occupies the measuring site. Use blue LED at its maximal intensity and set the transmittance for the blank to 100.0. Take measurements for samples and calibration solutions and write the transmittances into the table below. Calculate absorbance and prepare a calibration graph as demonstrated below.

		Calibration solutions
	Sample	1	2	3	4	5	6	7	8	9
g(Fe³⁺) [mg/L]	?	12.1	24.3	36.4	48.6	60.7	72.9	85.0	97.2	109.3
T
A

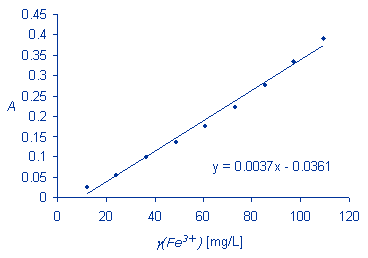
Use the linear equation obtained for your calibration data and calculate the iron concentration in the sample solution.

Note

If the absorbance of the sample solution exceeds the absorbance of the final calibration solution, the sample solution must by no means be diluted with water. This would shift the equilibrium and consequently cause erroneous results. The sample can only be diluted with a diluent solution. Dilution must be taken into account while calculating the iron content in the condiment sample.

The iron content per 100 g of the condiment sample is then calculated as follows:

m(Fe³⁺) =	g(Fe³⁺) · 0.013 L · 100 g

	m_sample

Worked out example

In our case 1.0041 g of a dry basil sample was taken for analysis. The transmittance of a sample solution measured against the blank using the blue LED was 77.5.

A = -log(77.5/100) = 0.1107

0.1107 = 0.0037 x - 0.0361

g(Fe³⁺) = x = 39.67 mg/L

m(Fe³⁺) =	39.67 mg · 0.013 L · 100 g	= 51.4 mg

	L · 1.0041 g

The iron content in a dry basil sample is 51.4 mg per 100 g of the condiment.